ווען מיר קויפן און ניצן קוואַדראַטישע רער, איז דער וויכטיקסטער פונקט צו באורטיילן צי דער פּראָדוקט טרעפט דעם סטאַנדאַרט דער ווערט פון R ווינקל. ווי ווערט דער R ווינקל פון קוואַדראַטישע רער ספּעציפֿיצירט אין דעם נאַציאָנאַלן סטאַנדאַרט? איך וועל צוזאַמענשטעלן אַ טאַבעלע פֿאַר אייער רעפֿערענץ.

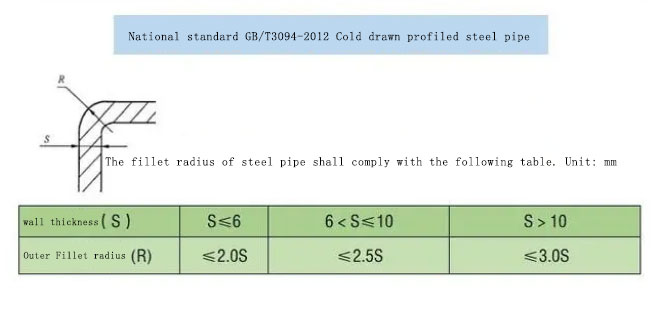
ווי אזוי צו רעכענען דעם R ווינקל פון א קוואדראט רער?
דער R ווינקל אין דער קוואַדראַטישער רער איז דער איבערגאַנגס-בויגן ביים פֿאַרבינדונגס-פּלאַץ פֿון צוויי פּלענער, וואָס איז בכלל דער האַלבער דיאַמעטער פֿון דער צענטער-ליניע פֿון דעם קרומען בויגן R ווינקל. דער ווערט פֿון דעם קרומען בויגן R איז בכלל 1.5~2.0 מאָל דער רער-דיאַמעטער. די גרייס פֿון דעם R ווינקל ווערט באַשטימט לויט דער וואַנט-גרעב פֿון דער קוואַדראַטישער רער. דער R ווינקל ווערט צעטיילט אין אינעווייניקסטן R ווינקל און אויסווייניקסטן R ווינקל. דער אינעווייניקסטער R איז בכלל 1.5~2 מאָל די וואַנט-גרעב. קוואַדראַטישע שטאָל-רערן מיט פֿאַרשידענע R ווינקלען קענען אויך פּראָדוצירט ווערן לויט די באַדערפֿנישן פֿונעם באַניצער.
למשל, פֿאַר אַ רעכטעקיקן שטאָל רער מיט אַ קייַלעכדיקן באָגן R, A=1.0 מם, דיאַגאָנאַל=1.15 מם, ווי ווייסט מען דעם ווינקל R? אויב עס איז אַ קוואַדראַטישע שטאָל רער מיט אַ באָגן, איז די קאַלקולאַציע מעטאָדע די זעלבע? אַ רעכטעק האט אַ לענג פון A און אַ ברייט פון B, אַ דיאַגאָנאַל פון C, און דער ראַדיוס פון די פיר ווינקל באָגן R איז גלייך. רעכנט אויס די גרייס פון R לויט דער פאלגענדער פאָרמולע: (C/2-R) ^ 2=(A/2-R) ^ 2+(B/2-R) ^ 2 C ^ 2/4-CR+R ^ 2=A ^ 2/4-AR+R ^ 2+B ^ 2/4-BR+R ^ 2 4R ^ 2-4 (A+BC) R+(A ^ 2+B ^ 2-C ^ 2)=0.
עס איז דא וויכטיג צו באטאנען אז דער R ווינקל פון דער אונטערשטער רעכטעקיגער רער באציט זיך נישט צום בויגן, נאר צום צענטער ווינקל. דער בויגן באציט זיך צו א סעגמענט אויפן ארומקרייז, און דער איינגעשלאסענער ווינקל פון דער ליניע צווישן די צוויי עקן פונעם בויגן און דעם צענטער איז דער צענטער ווינקל. ווייל דער ארומקרייז פון א קרייז איז 2πR און זיין קארעספאנדירנדיקער צענטער ווינקל איז 2π, איז די בויגן לענג וואס קארעספאנדירט צום איינהייט צענטער ווינקל 2πR/2π=R. דעריבער באקומט מען די בויגן לענג וואס קארעספאנדירט צו יעדן צענטראלן ווינקל a (ראדיאן איינהייט)=aR. די מעסט מעטאדן און געצייג פארן קוואדראטישן רער R ווינקל שליסן איין R גיידזש און פראיעקטאר. דער R גיידזש קען גענוצט ווערן פאר דיקע פונקטן, דער פראיעקטאר פאר פיינע פונקטן, און דער CMM פאר הויכע באדערפענישן.
יואַנטאַי'ס רעכטעקיקע רער פּראָדוקטן קענען דערגרייכן העכערע פּינקטלעכקייט, און ווערן וויידלי געניצט אין בנינים, ערטער, בריקן, עקוויפּמענט, לאַסט-טראָגנדיקע און אַנדערע אינדוסטריעלע און לעבן סצענעס.
אויב קלאַסיפיצירט לויט סצענאַר, קען מען עס צעטיילן אין די פאלגענדע קאַטעגאָריעס:
יואַנטאַי שטאָל ליידיק אָפּטיילונג פֿאַר שיף-בילדינג
יואַנטאַי שטאָל רער פֿאַר שטאָל סטרוקטור
יואַנטאַי שטאָל רער פֿאַר אָראַנזשעריי
פּאָסט צייט: 15 דעצעמבער 2022









